AES나 DES와 같은 암호화 알고리즘을 이용해서 보안 통신을 하기 위해서는 암호키가 필요하다. 암호키를 통해서 제 3자가 이를 해독하기 어렵게 만드는것이다. 암호키를 제 3자가 알면 암호를 깨고 데이터를 복호화할 수 있기 때문에 안전하게 암호화 키를 공유할 필요가 있다. 디피 헬만은 위와 같은 암호화 통신에서 안전하게 키를 교환하는 방법 중 하나로 TLS에서 많이 사용해 왔다.

최근에 TLS를 공부하면서 타원곡선 디피 헬만(Elliptic Curve Diffie Hellman)에 대해 알아보고 싶어서 공부를 시작했다. 일반적으로 타원곡선 디피 헬만은 적은 CPU와 메모리 자원과 더 작은 키 값으로도 일반 디피 헬만에 비해 안전한것으로 알려져 있다. 일반 디피 헬만의 키 사이즈가 2048bit면 ECDH에서는 224bit 사이즈의 키로 같은 안전성을 보장한다.

ECDH의 원리 이해를 위해서는 정수론에 대한 이해가 필요했다. 따라서 글을 모듈러 연산과 군, 이산로그 그리고 타원곡선 디피 헬만 순으로 나눴다.

Modular 연산 (나머지 연산)

정수를 정수와 나누면 나머지가 발생한다. 거의 모든 프로그래밍 언어에 항상 빠지지 않고 등장하는 흔한 이항연산자다.

a는 피제수, N은 제수, b는 나머지다. Modular 연산의 예를 들면 아래와 같다.

알지 못할 수 있지만 음수에 대한 나머지 연산도 가능하다. 음수의 나머지 연산을 계산할 경우, 피제수의 값을 양수라 생각하고, 제수의 차를 구한다. 예를 들어 \(-40 \mod 17\)의 경우 40의 mod 17 값인 6과 17의 차인 11이 정답이다.

합동

Modular 연산에서의 합동은 나머지가 같은 값들을 의미한다. 예를들어, 17에 대하여, 40과 합동인 수는 6, 23, 57, …등이다. 이를 식으로 나타내면 \(40 \equiv 6 \mod 7\)이 된다. 이 개념을 갖고 식에 적용하면 합동식이 되는데 예를들면 \(3x \equiv 7 \mod4\) 과 같이 적을 수 있다. 이를 풀이하면 3의 배수 중에서, 4와 나눴을때 나머지 값이 7과 4를 나눈 나머지와 같은 수를 의미한다.

Modular 역수

\(40 ^{-1} \equiv x \mod 17\)에서 \(x\)는 얼마일까? 곱샘 연산자에서는 연산을 진행해도 같은 수가 나오는 항등원은 1이다. (덧샘에서는 0) \(40 ^{-1}\)과 \(40\)은 서로 곱하면 항등원인 1이 나오는 곱샘에서의 역원 관계에 있다. 따라서 17에 대한 나머지 연산에서 40과 곱했을때 연산 결과가 1이 나오는 값이 40의 역원인 \(40 ^{-1}\)과 같은 값입니다. 예를들어 40의 법 17에 대한 역수는 3이다.

따라서 \(40 ^{-1} \equiv 3 \mod 17\)이라 할 수 있다.

군 (Group)

군은 하나의 이항 연산자에 대해서 특수한 조건을 갖고 있는 수의 집합이다.

1. 군은 정의된 연산자에 대해서 닫혀있어야 한다.
2. 연산자에 대해서 결합법칙이 성립되어야 한다.
3. 군 안에는 항등원과 역원이 있어야 합니다.

위와 같은 조건을 충족하는 집합의 사례를 들어보자. 모든 정수는 덧셈에 대해서 군을 이룬다. 위 조건에 부합하는지 알아보자, 우선 정수를 정수와 더하면 정수가 나올것이다. 또한 덧샘은 결합법칙이 성립하는 연산이다. 그리고 정수 안에는 덧샘의 항등원인 0이 있고, 역원인 음수가 있다. 예를들면 42의 역원은 -42이고 항등원은 0이다. 증명하는 방법이야 있겠지만 모든 정수가 덧셈에 대해서 군을 이룬다는 것은 자명한 사실이다. 정수와 같이 덧셈에 대한 군을 덧셈군이라 부른다. 이와 마찬가지로 곱샘에 대해서 군이 성립하면 곱샘군이라 할 수 있다.

그러면 정수는 곱셈군이라 부를 수 있을까? 아쉽게도 그렇지 않다. 우선 역원이 없다. 예를 들면 2의 곱셈에 대한 역원은 1/2인데 이는 정수가 아닌 유리수이다. 그렇다면 유리수는 곱셈군을 이룬다 볼 수 있는가? 이 또한 그렇지 못 한다. 유리수에는 0이 있는데, 0은 곱셈에 대한 역원이 존재하지 않는다. (1/0은 계산할 수 없다.) 따라서 0을 제외한 유리수가 곱셈군을 이룬다 볼 수 있다.

Modular N에 대한 정수 ( \(\mathbb{Z}/n\mathbb{Z}\) )

Modular N에 대해서 모든 정수의 나머지의 집합을 이야기한다. 예를 들면 8에 대한 나머지 집합인 \(\mathbb{Z}/8\mathbb{Z}\) 이라 표기하고 0, 1, 2, … 7까지의 숫자들이다. Modular 연산을 한 정수 집합은 덧셈군이 될까? 덧셈군은 성립한다. 예를들면 \(3 + 7 \mod 8\)의 값이 \(\mathbb{Z}/8\mathbb{Z}\)안에 있어야하고, 역수와 항등원이 존재해야한다. 우선 정수를 정수끼리 더하면 정수가 나올것이다. 그리고 항등원은 0이 있고 계산하면 0이 나오는 역원 또한 존재한다. Modular 8에 대한 정수 집합에서 보면 7에게는 1이 역원이고, 5에게는 3이 역원이 될 것이다. 모든 Modular N에 대한 정수는 일반 정수와 마찬가지로 덧셈군이 성립된다. 그렇다면 곱셈군도 성립할 수 있을까?

우선 정수와 마찬가지 이유로 0은 제외해야 한다. 하지만 Modular N에 대한 정수에서는 0을 제외해도 문제가 숫자가 있다. 2, 4, 6입니다. 이 수 들은 어떤 수와 곱했을때 8의 배수가 될 여지가 있다. 그러면 Modular 연산하면 제외된 0이 나온다. 6으로 예를 들면,

24는 8의 배수임으로, 나머지 값이 0이 나오고 0을 제외한 집합에 대해서 닫혀있지 않은 연산이 된다. 이렇듯 곱셈 연산에 닫혀 있기 위해서는 0, 2, 4, 6을 제외한 1, 3, 5, 7이 Modular N에 대한 곱셈군(Multiplicative group of integers modulo n)이 된다. 기호로는 \((\mathbb{Z}/n\mathbb{Z})^\times\) 이렇게 표기한다.

Modular N에 대한 곱셈군(Multiplicative group of integers modulo n)

위에서 확인한 곱셈군인 1, 3, 5, 7은 8과 어떤 관계에 있는가? 곱셈군에 포함되지 않았던 값들은 다른 수와 곱했을때 8의 배수가 될 여지가 있는 수였다. 따라서 어떤수와 곱해도 8이 될 여지가 없는 수가 된다는 의미고, 이 말은 8과 서로소(두 수의 최대공약수가 1) 관계에 있다는 의미가 된다.

N이 서로소가 많고 큰 수 라면, Modular N에 대한 곱셈군의 크기(order)가 커진다. 서로소가 많은 수는 소수가 있다. 소수는 모든 정수와 서로소 관계에 있다. 예를 들면 소수 7은 \(\mathbb{Z}/7\mathbb{Z}\)는 0, 1, 2, 3, 4, 5, 6이 있고 이 중 0을 제외하면 모두 서로소 관계에 있다. 따라서 0을 제외하면 모두 \(\mathbb{Z}/7\mathbb{Z}^\times\)에 포함되어 있단 의미가 된다.

이산로그 문제 (discrete logarithm problem)

암호화 알고리즘에게 있어서 중요한 문제는, 암호화를 하는 과정은 굉장히 간단하고 빠르게 진행되어야하지만 이를 복호화하는 과정은 매우 어려워야한다. 이를 일방향 함수(One-way function)라 이야기하는데 이산 로그 문제는 아주 전형적인 One-way function이다.

위에서 이야기한 \(\mathbb{Z}/7\mathbb{Z}^\times\)를 생각해보자, 이 집합은 1, 2, 3, …6까지의 수를 포함하고 있고, 모듈로 곱셈에 대해서 닫혀 있다. 따라서 거듭제곱 연산에 대해서도 닫혀있다 할 수 있다. 이를 이산 거듭제곱이라 이야기하는데, 예를 들어, \(3^6 \mod 7\)한 값은 729을 7로 나눈 나머지 1가 된다.

여기서 결과값이 1이 되는 최솟값인 지수가 이산로그 값이다. 지수를 알고 계산하면 결과값을 계산하는데에 일반적인 연산에 가깝지만, 결과와 지수 연산의 밑만 가지고선 지수를 추론하는 과정은 1부터 시작해서 하나하나 비교하는 방법 외에는 없다.

\(\mathbb{Z}/7\mathbb{Z}^\times\)의 경우 군의 크기가 6으로 작지만 7 대신 굉장히 큰 소수를 사용하면 군의 크기가 커지고, 이산 로그 문제를 해결하는 알고리즘은 군의 크기의 자릿수에 지수적인 복잡도를 갖고 있다. 이를 조금 효율적으로 찾는 방법은 있지만 의미있게 빠른 방법은 아직 없는것으로 알려져 있다. 또한 밑(위의 예제의 경우엔 3)을 정의하는 것이 중요한데, 밑 값을 제곱하여 modular 연산한 결과의 값이 \(\mathbb{Z}/n\mathbb{Z}^\times\)의 모든 원소를 포함해야 추론이 어려워지기 때문이다. 위와 같은 밑을 Primitive root라 이야기한다. 따라서 많은 보안 통신을 하는 프로그램들이 \(\mathbb{Z}/n\mathbb{Z}^\times\)의 소수 N과 Primitive root값인 g값에 대해선 사전에 정의해두고 사용한다.

결론적으로 일반적인 이산 로그 문제는 Modular N에 대한 곱셈군에서 곱셈의 반복 연산인 제곱의 역연산 값 로그 값을 구하기 어려운 문제를 이야기한다. 이는 RSA, 디피 헬만에 유용하게 쓰인다.

타원곡선

타원곡선이란 \(y^2 = x^3 + ax + b\) 꼴의 형태로 나타내지는 곡선을 의미한다. 그래프로 표현하면 아래와 같은 꼴이 된다.

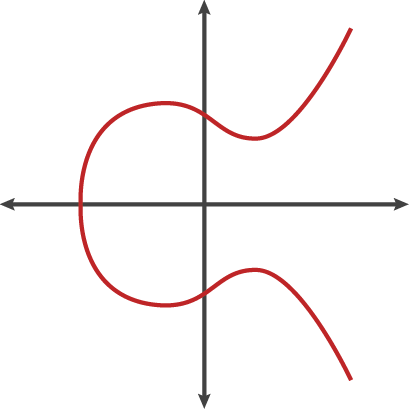
그래프의 모양이나 방정식의 형태나 둘다 타원과는 크게 상관 없고, 타원의 둘레를 구하기 위한 적분에서 이름이 유래되었다고 한다.

타원 곡선의 연산

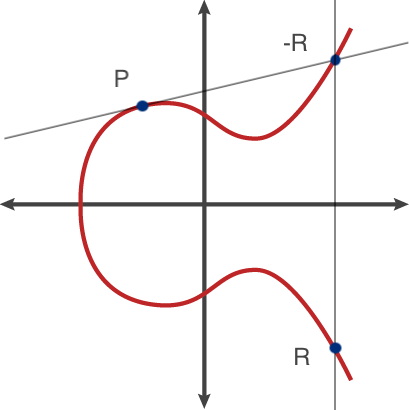
타원 곡선에서는 두 점에 대한 특이한 덧셈 연산이 존재한다. 점 P와 Q를 타원 곡선에서 더한 결과 R은 아래의 그림과 같다.

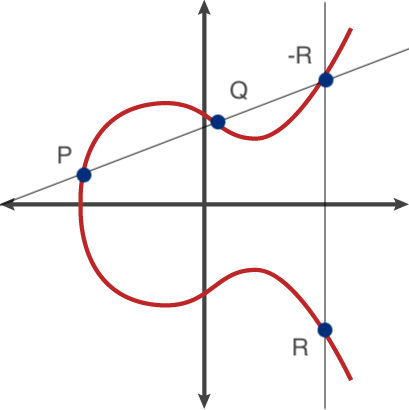
P와 Q를 지나는 직선을 긋고 이 직선이 타원 곡선과 만나는 점에 대해서 X축 대칭점이 R의 결과다. P의 좌표를 \((x_P, y_P)\) Q의 좌표를 \((x_Q, y_Q)\), R의 좌표를 \((x_R, y_R)\)로 두고 R의 좌표를 계산하는 방법은 아래와 같다.

위 식을 보면 \(y_P\) 와 \(y_Q\)가 다른데, \(x_P\) 와 \(x_Q\)가 같으면 s의 값이 무한으로 발산한다는 것을 알 수 있다. 이 말은 P와 Q가 동일한 X 좌표를 갖고 있으면 R의 값을 구할 수 없다는 이야기다. 그림으로만 봐도 구할 수 없게 생겼다.

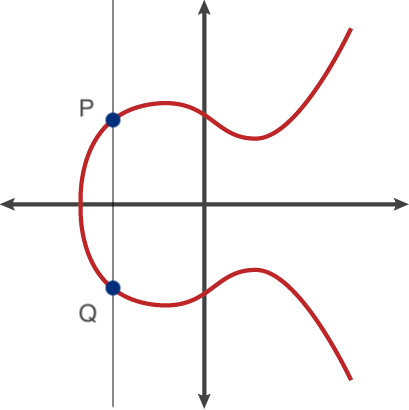
위와 같은 경우 R의 점을 무한점(∞)이라 정의한다. 무한점의 성질에 대해서 한 가지 더 정의하면 타원 곡선의 덧셈 연산 정의가 끝난다. P가 ∞인 경우에 P + Q에 대한 결과 문제다. 이 경우엔 Q를 지나고 X축과 직교하는 선을 그리고 이때 타원 곡선과 만나는 점을 -R로 두고 위와 같은 방식으로 X축과 대칭점인 R을 구한다. 이렇게 구한 값은 Q와 동일하다. 그림으로 보면 이해하기 쉽다.

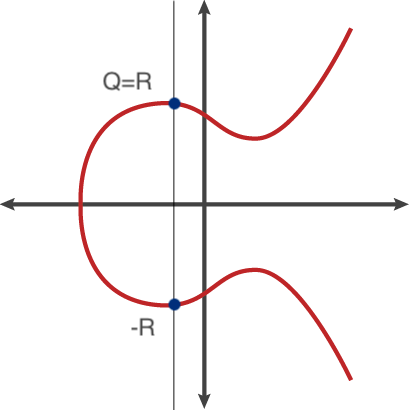
그렇다면 \(y_P\) 와 \(y_Q\)가 같고, \(x_P\) 와 \(x_Q\)도 같은 즉, P를 두번 더한 경우는 어떻게 계산할 수 있을까? 이때는 타원 곡선 위의 점 P와 접하는 직선과 교차하는 점이 R값이 된다.

이를 수식으로 표현하면 아래와 같다. 이 때 a는 \(y^2 = x^3 + ax + b\)의 a값이다.

위에서 이야기 한 타원 곡선에 대한 연산을 정리하면

1. P와 Q를 지나는 직선과 만나는 점의 X축 대칭점을 R로 계산한다.
2. P와 Q를 지나는 직선이 X축과 직교하면 R은 무한점(∞)이다.
3. 무한점(∞)과 점 P를 더하면 결과값 R은 P와 같다.

와 같이 정리할 수 있다. 위 정리를 보면 무한점은 위에서 이야기한 항등원이란 사실을 알 수 있다. 이 때의 역원은 X축의 대칭점일 것이다. 따라서 점 P의 X축 대칭점은 -P라 이야기할 수 있다. 무한점을 포함하면 \(y^2 = x^3 + ax + b\)을 지나는 모든 점에 대해 해당 연산은 닫혀 있고, 결합법칙이 성립한다고 한다(이 부분은 증명이 어려움). 따라서 타원 곡선과 무한점을 포함한 집합은 이 연산에 대해서 군을 이룬다.

타원곡선의 이산로그 문제

타원곡선의 연산을 사용해서 점 P를 P와 더하는 것을 2P라고 정의한다면 P를 세번 더한 값을 3P로 나타내면 k번 더한 결과 Q를 \(kP\)라 나타낼 수 있다.

위에서 이야기 했던 이산로그 문제와 마찬가지로 Modular N에 대한 타원곡선 덧셈군에 대해서 반복 연산인 곱셈의 역연산 값을 추론하기 어렵다. 따라서 P와 k를 갖고 Modular N연산을 한 Q를 계산하는 것은 쉽지만, Q와 P만 가지고는 k값을 찾는것은 굉장히 어렵단 이야기다. 예를 들면 타원곡선을 \(y^2 = x^3 + 2x + 2 \mod 17\)로 두고 P를 (5, 1)로 정의하자, 이때 결과값 Q를 P를 4번 더한 값은 (3, 1)이 된다. 만약 Q값인 (3, 1)과 P값인 (5, 1)만 보고 몇 번 더한것인지 추론하려 한다면, 이는 굉장히 어렵다는 이야기다(이산로그 문제).

따라서 일반적인 이산로그 문제와 마찬가지로 P값과 Modular N값을 잘 정의하면, 이를 일반적인 디피 헬만과 마찬가지 방법으로 암호키 교환 알고리즘에 사용할 수 있다.

타원곡선 디피 헬만

일반 디피 헬만과 마찬가지로 Alice와 Bob 둘이 통신하고 이를 중간에서 Eve가 훔쳐보고 있다 가정하자. 우선 Alice와 Bob이 각자의 비밀키를 만든다. 이를 \(\alpha\), \(\beta\)라 하자. 그리고 기준이 되는 타원곡선 함수를 \(y^2 = x^3 + ax + b \mod N\)로 정의하고, 기준점을 G라 하자. 그러면 Alice와 Bob, 그리고 훔쳐보는 Eve는 모두 a, b, N, G 값을 알고 있다. 이 때 Alice와 Bob은 각자 공개키를 만들어서 나누어 갖는다.

Eve는 A나 B로 부터 \(\alpha\), \(\beta\)를 추론할 수 없어 K를 구할 수 없지만 Alice와 Bob은 받은 공개키 값을 각자의 비밀키 값과 곱해서 이를 알아낼 수 있다.

예를 들어보자, 타원곡선을 \(y^2 = x^3 + 2x + 2 \mod 17\)로, G를 (5, 1)로 정의하자. 이 때 Alice와 Bob이 스스로 비밀키를 고르고 공개키를 나누는 과정을 보면 아래와 같다.

따라서 Eve가 키 값 K를 알아내기 위해선 \(y^2 = x^3 + 2x + 2 \mod 17\)의 G에 대한 모든 경우의 수를 알아내 A나 B값을 통해 비밀키를 구할 수 있으면 된다.(이산로그 문제)

References

• 모듈러 연산(Modular Arithmetic)
• 원들대 01: 군의 정의와 아벨군의 예제
• 이산로그
• Elliptic Curve Diffie Hellman